Research News

This sections contains quick summaries about selected research articles.

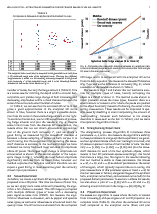
Unleashing transformers: parallel token prediction with discrete absorbing diffusion for fast high-resolution image generation from vector-quantized codes

Summary

Accepted at ECCV. We propose a novel parallel token prediction approach for generating VQ image representations that allows for significantly faster sampling than autoregressive approaches. Our approach achieves state-of-the-art results and can generate high-resolution images surpassing the original training data's resolution.

Examples of unconditional samples from our models

Approach

We utilize a Vector-Quantized (VQ) image model to compress images into a discrete latent space. An absorbing diffusion model then learns the latent distribution, allowing us to generate high-resolution images rapidly, without the need for time-consuming autoregressive methods.

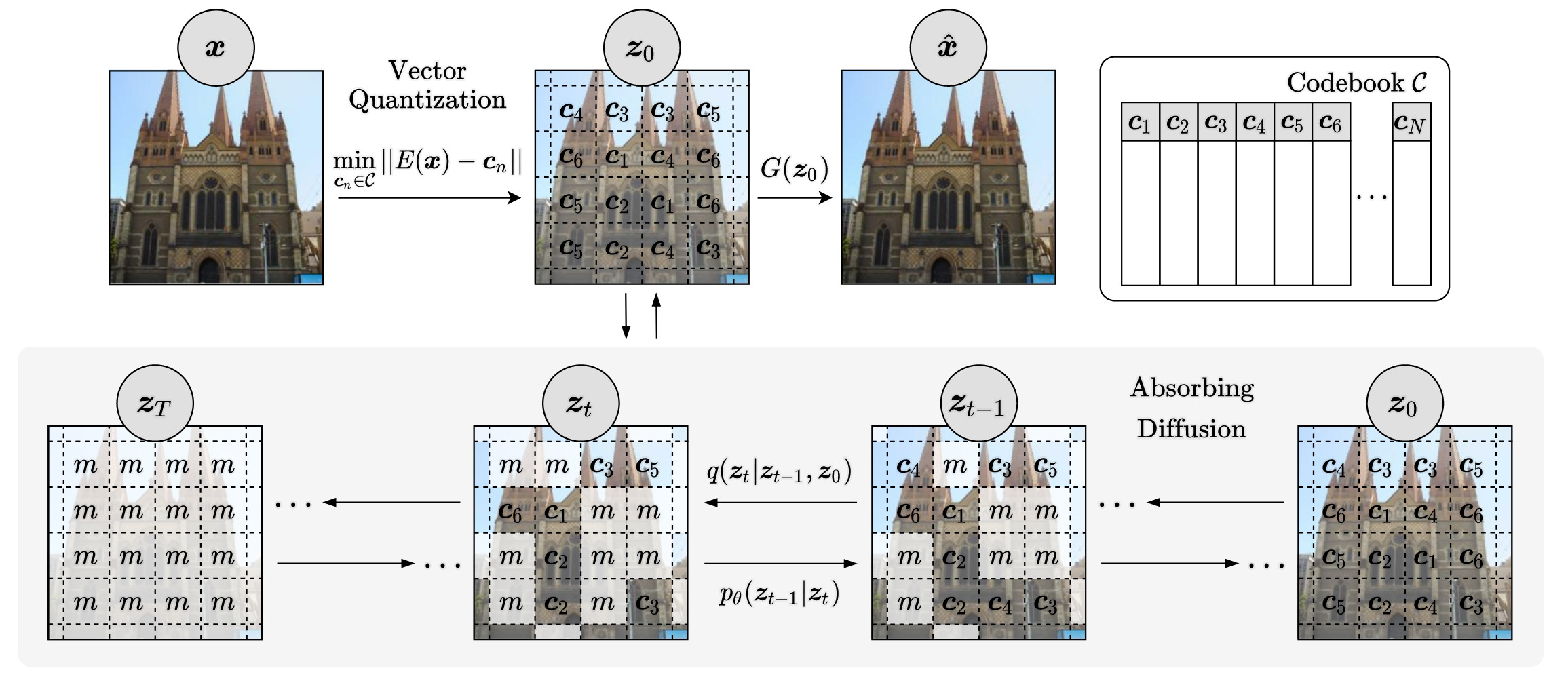
Evaluation

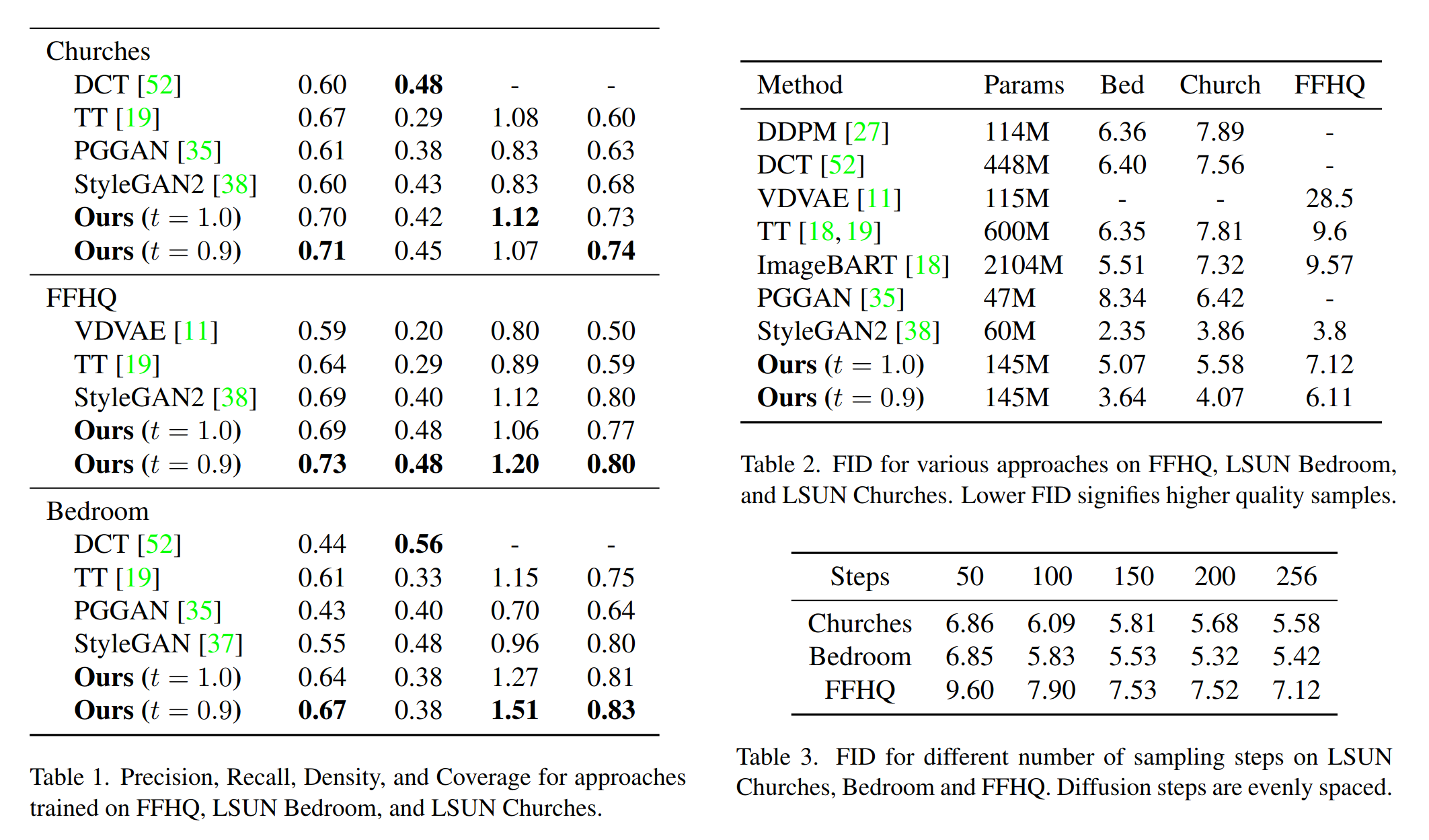
Our method has been rigorously evaluated on multiple high-resolution datasets, including LSUN Churches, LSUN Bedroom, and FFHQ. Despite its efficiency and reduced parameter count, our approach achieves comparable or better results against other VQ image models.

We also support outpainting (synthesise image regions outsdie the training data), inpainting, and control over the sample diversity.

Citation

Please cite the article with:


      @inproceedings{bond2022unleashing,
  title={Unleashing Transformers: Parallel token prediction with discrete absorbing diffusion for fast high-resolution image generation from vector-quantized codes},
  author={Bond-Taylor, Sam and Hessey, Peter and Sasaki, Hiroshi and Breckon, Toby P and Willcocks, Chris G},
  booktitle={European Conference on Computer Vision},
  pages={170--188},
  year={2022},
  organization={Springer}
}

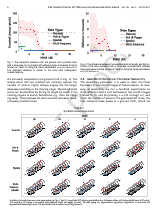
Deep learning protein conformational space with convolutions and latent interpolations

This work has been accepted at Physical Review X, 2021. We present a convolutional neural network that learns a continuous conformational space representation from example structures, and loss functions that ensure intermediates between examples are physically plausible. We show that this network, trained with simulations of distinct protein states, can correctly predict a biologically relevant transition path, without any example on the path provided.

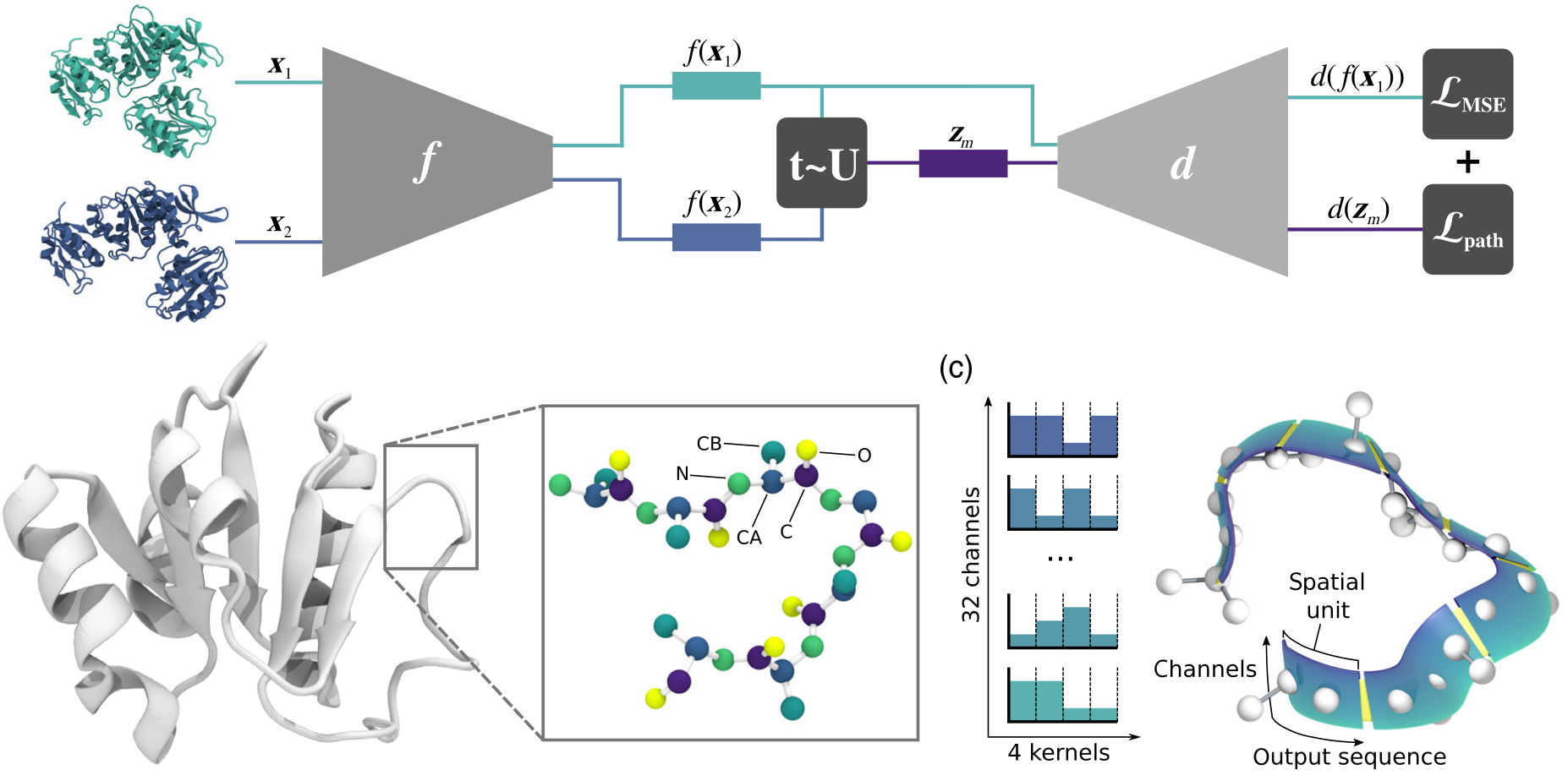
Proteins carry out a range of essential biological functions including catalysis, sensing, motility, transport, and defense. These molecules function independently or in unison with other molecules, such as DNA, drugs, or other proteins. To perform these functions, a protein must often change its shape (or conformation), but identifying the possible conformations of a protein is not an easy task. We present a methodology that combines molecular simulation and machine learning to discover transition paths between protein conformational states.

Current experimental techniques provide a good picture of the most stable conformations and little to nothing on the transition path or intermediate states. Despite the importance of these intermediate conformations for pharmaceutical drug targeting purposes, determining them with high reliability remains a challenging problem. We overcome this hurdle with a neural network that can generate new protein conformations after being trained with examples from experiments or molecular simulations. The network is capable of generating structures that respect physical laws.

Citation

Please cite the article with:


  @article{ramaswamy2021deep,
  title     = {Deep Learning Protein Conformational Space with Convolutions and Latent Interpolations},
  author    = {Ramaswamy, Venkata K. and Musson, Samuel C. and Willcocks, Chris G. and Degiacomi, Matteo T.},
  journal   = {Phys. Rev. X},
  volume    = {11},
  issue     = {1},
  pages     = {011052},
  numpages  = {13},
  year      = {2021},
  month     = {Mar},
  publisher = {American Physical Society},
  doi       = {10.1103/PhysRevX.11.011052}
}

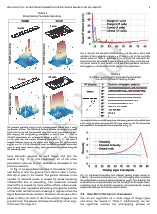
Gradient origin networks

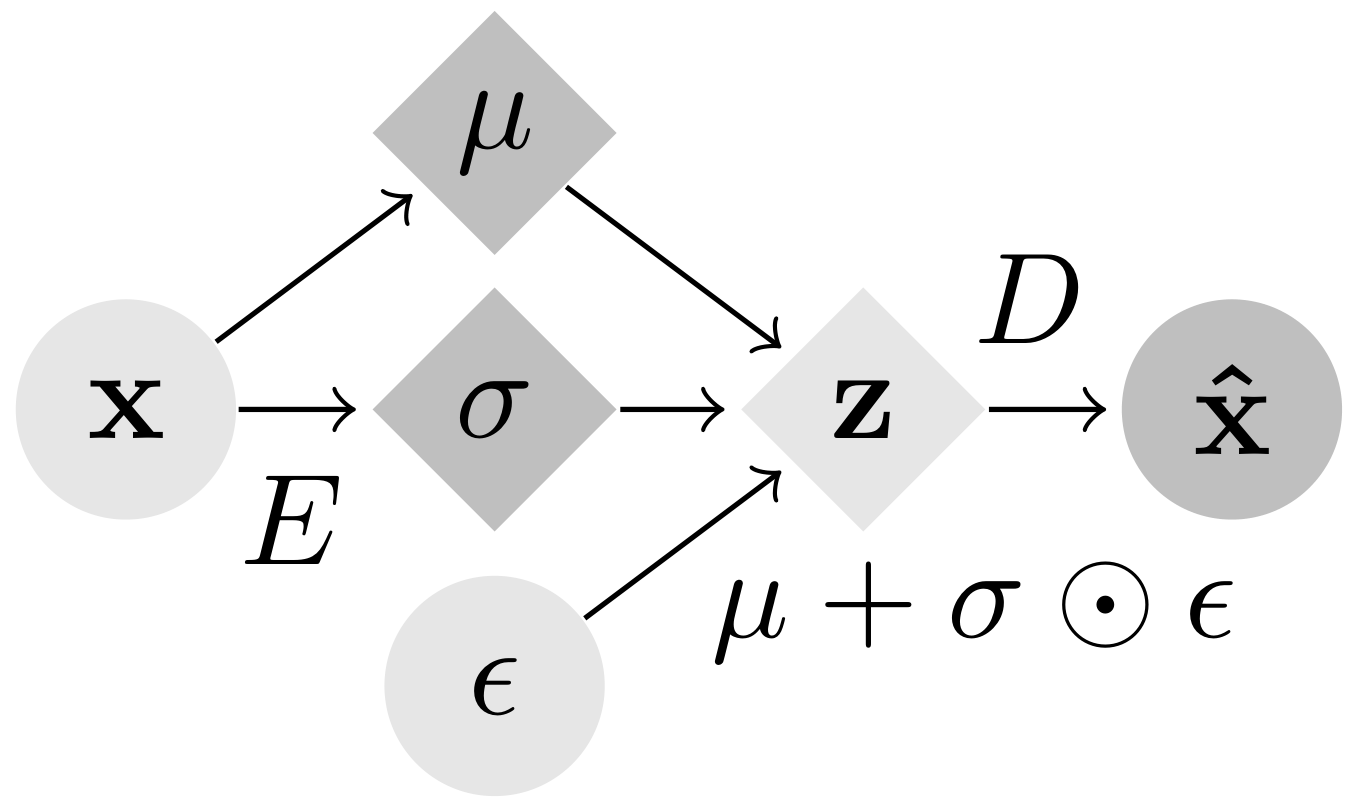
This work has been accepted at ICLR 2021. Gradient Origin Networks (GONs) are comparable to Variational Autoencoders in that both compress data into latent representations and permit sampling in a single step. However, GONs use gradients as encodings meaning that they have a simpler architecture with only a decoder network:


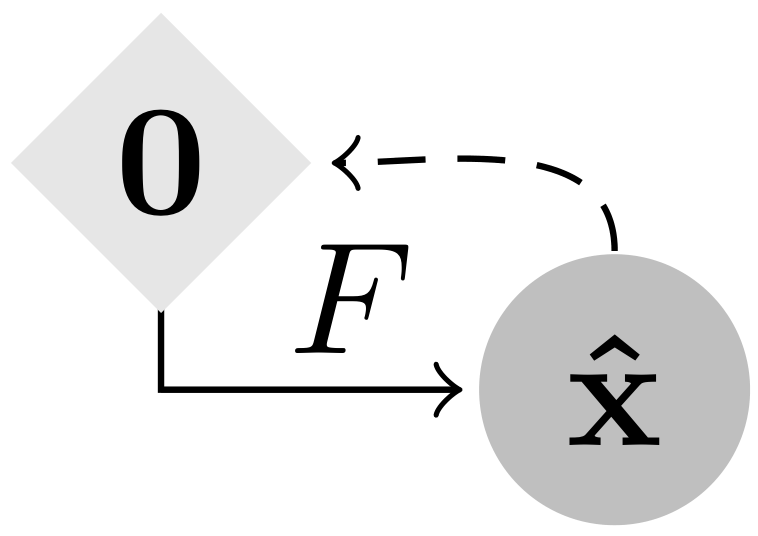Variational Autoencoder	Gradient Origin Network

In Gradient Origin Networks, unknown parameters in the latent space are initialised at the origin, then the gradients of the data fitting loss with respect to these points are used as the latent space. At inference, the latent vector can be sampled in a single step without requiring iteration. Here are some random spherical interpolations showing this:


MNIST	FashionMNIST	COIL20

In practice, we find GONs to be parameter-efficient and fast to train. For more details, please watch the YouTube video and read the paper in the links in the project page. Theres also a google colab link if you want to try running the code in your browser.

Citation

Please cite the article with:


  @inproceedings{bond2020gradient,
  title     = {Gradient Origin Networks},
  author    = {Sam Bond-Taylor and Chris G. Willcocks},
  booktitle = {International Conference on Learning Representations},
  year      = {2021},
  url       = {https://openreview.net/pdf?id=0O_cQfw6uEh},
  keywords  = {Conference}
}

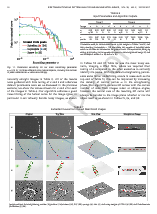
Multi-scale segmentation and surface fitting for measuring 3D macular holes

Selected photos from the paper below:

Click to go to full publication on IEEE Explore.

Abstract

Macular holes are blinding conditions, where a hole develops in the central part of retina, resulting in reduced central vision. The prognosis and treatment options are related to a number of variables, including the macular hole size and shape. High-resolution spectral domain optical coherence tomography allows precise imaging of the macular hole geometry in three dimensions, but the measurement of these by human observers is time-consuming and prone to high inter- and intra-observer variability, being characteristically measured in 2-D rather than 3-D. We introduce several novel techniques to automatically retrieve accurate 3-D measurements of the macular hole, including: surface area, base area, base diameter, top area, top diameter, height, and minimum diameter. Specifically, we introduce a multi-scale 3-D level set segmentation approach based on a state-of-the-art level set method, and we introduce novel curvature-based cutting and 3-D measurement procedures. The algorithm is fully automatic, and we validate our extracted measurements both qualitatively and quantitatively, where our results show the method to be robust across a variety of scenarios. Our automated processes are considered a significant contribution for clinical applications.

Overview

Given a 3D OCT image of a Macular Hole, this paper presents a fast and accurate fully-automated 3D level set segmentation method.

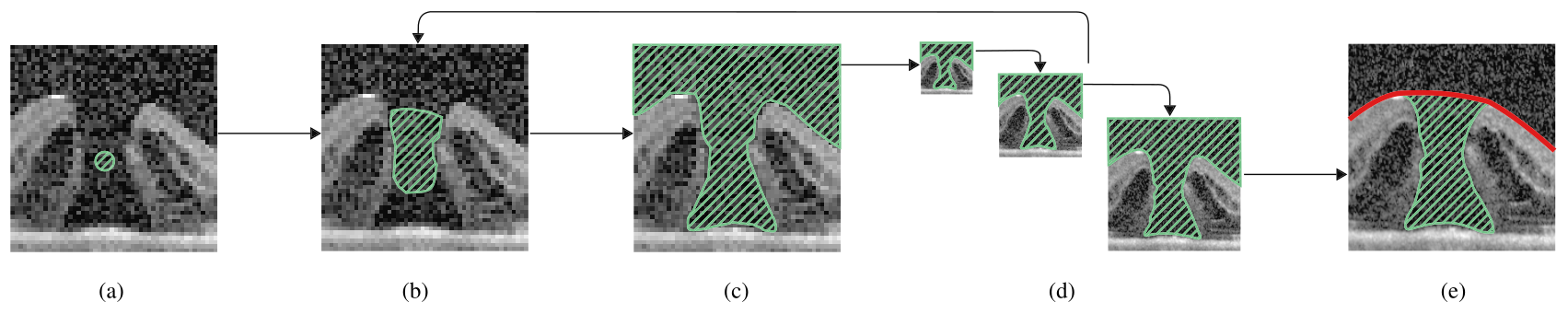
The method automatically outputs several metrics and measurements using novel methods, and is shown to give state-of-the-art performance in comparrison to previous approaches.

Citation

Please cite the article with:

@article{nasrulloh2017multiscale,
  author   = {A. V. Nasrulloh and C. G. Willcocks and P. T. G. Jackson and C. Geenen and M. S. Habib and D. H. W. Steel and B. Obara},
  journal  = {IEEE Transactions on Medical Imaging},
  title    = {Multi-scale Segmentation and Surface Fitting for Measuring 3D Macular Holes},
  year     = {2018},
  month    = {2},
  volume   = {37},
  pages    = {580-589},
  doi      = {10.1109/TMI.2017.2767908},
  ISSN     = {0278-0062}
}

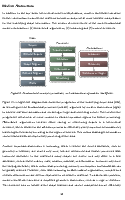
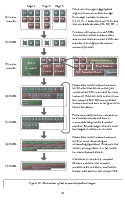
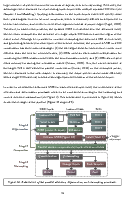
Extracting 3D parametric curves from 2D images of helical objects

Chris Willcocks, Philip Jackson, Carl Nelson, and Boguslaw Obara

Click to go to full publication on IEEE Explore.

Abstract

Helical objects occur in medicine, biology, cosmetics, nanotechnology, and engineering. Extracting a 3D parametric curve from a 2D image of a helical object has many practical applications, in particular being able to extract metrics such as tortuosity, frequency, and pitch. We present a method that is able to straighten the image object and derive a robust 3D helical curve from peaks in the object boundary. The algorithm has a small number of stable parameters that require little tuning, and the curve is validated against both synthetic and real-world data. The results show that the extracted 3D curve comes within close Hausdorff distance to the ground truth, and has near identical tortuosity for helical objects with a circular profile. Parameter insensitivity and robustness against high levels of image noise are demonstrated thoroughly and quantitatively.

Overview

In this paper, we take a 2D image of a helical object and automatically fit a 3D curve to it. To do this, we first segment and straighten the helical object and then we find peaks on the boundaries of the helical object. The curve fits through these peaks.

Key processes

• Image segmentation
• Image straightening
• Curve fitting

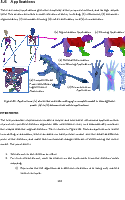
Applications

The primary applications of this research are to retreive a 3D model of 2D images of helical objects, e.g. for collecting measurements, where 3D imaging is currently too expensive or impossible.

At a micro scale:

Biology and medicine (e.g. Spirulina, Spirochaetes, sperm, bacterial macrofibers, microtubules, keratin, DNA, dynamin).
Nanotechnology (e.g. helical nanostructures, such as: nanosprings and graphitic carbon microtubules).

At a macro scale:

Medicine (e.g. umbilical cord).
Biology (e.g. climbing plants, twining vines, twisted trees, seashells, Arabidopsis root).
Cosmetics industry (e.g. hair).
Engineering (e.g. screws, coils, springs, synthetic fiber ropes).

Additional output 3D metrics include:

• Tortuosity
• Radius
• Pitch
• Length

Areas for Future Research

To our knowledge, this is the first work that can automatically and robustly fit a 3D parametric curve to a single 2D image of a helical object. We believe there are several areas for improvement:

In the future, a simpler algorithm for fitting 3D parametric curves to noisy 2D data will be found that doesn't require the straightening process. This will be faster and more robust, without the need for several parameters.
The future research should focus on robustly capturing 2D polylines from 2D images and transforming the polyline geometry to capture the 2D helical structure. Extending the 2D polyline to a 3D piecewise helix is a well-researched area with good solutions.

Code Usage

Our code is written in MATLAB. To use it, clone the github repository somewhere and add it to your MATLAB workspace, then simply edit the image, set the parameters and run the script main.m.

I = imread('leptospira.png');
if (size(I,3) > 1); I = rgb2gray(I); end;                                   fprintf('\tdone!\nSegmenting...');
% Adjust algorithm parameters (see paper for detailed explanations)
straighten  = true;
sigma       = 0.01;             % smoothing amount, try 0.15 for 'licerasiae.png'
d           = max(size(I))/20;  % minimum distance between peaks, set to 0 for images with lots of coils
delta       = 50;
omega       = max(size(I))/20;
omicron     = 30;
push        = true;

% Run our algorithm steps
[c,B]       = part1_segment(I);                                             fprintf('\t\tdone!\nStraightening... ');
[Bp,T]      = part2_straighten(B,c,delta,omega,omicron,straighten);         fprintf('\tdone!\nFitting... ');
[p]         = part3_fitting(Bp,sigma,d,push);                               fprintf('\t\t\tdone!\nUndo transforms... ');
[tp]        = part4_undo_transforms(p,T,straighten);                        fprintf('\tdone!\n');

% Create our cubic spline (cs) through the transformed curve control points tp
cs = cscvn(tp);
cs = fnplotdense(cs);

% We can also use the straight spline (ss) from control points p
ss = cscvn(p);
ss = fnplotdense(ss);

% Example 3D metrics from the straight spline
tortuosity  = sum(sqrt(sum(diff(ss,1,2).^2,1))) / sqrt(sum((ss(:,end) - ss(:,1)).^2));
peaks       = floor(length(p)/2);

Github:

Sources for this paper can be downloaded here. These are well-documented and reflect the paper's method.

Citation

Please cite our paper:

@article{willcocks-2016-extract-3d-curve,
  author   = {C. Willcocks and P. Jackson and C. Nelson and B. Obara},
  journal  = {IEEE Transactions on Pattern Analysis and Machine Intelligence},
  title    = {Extracting 3D Parametric Curves from 2D Images of Helical Objects},
  year     = {2016},
  volume   = {PP},
  number   = {99},
  pages    = {1-1},
  doi      = {10.1109/TPAMI.2016.2613866},
  ISSN     = {0162-8828},
  month    = {},
}

Sparse volumetric deformation

Selected photos from 2013 thesis below:

Click to go to full publication on Durham e-thesis Link.

Overview

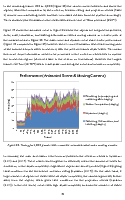
This thesis was split into two sections: 1. my attempt to come up with a way to render large amounts of animated voxel models, and 2. my skeletonization work.

The renderer itself was somewhat unique and written mainly in CUDA with C++. Very briefly, the key ideas were using skeleton-mapped sparse voxel octrees for each animated model stored on disk, and paged through the memory-levels at resolutions of interest, then the renderer itself makes heavy use of instancing and top-down occlusion culling. Although it was reasonably efficient at rendering large scenes, the limitation was overly using parallel stream-compaction to discard unimportant chunks, and relying on forward transformations for the animation. It had a few key contributions, such as simple solutions to prevent holes/gaps with forward transformations by altering the rendered hierarchy (lowering the voxel resolution to fill gaps).

Future Work

I had more success using implicit surfaces, e.g. storing the distance transforms of 3D models in 3D texture memory at multiple resolutions. Animation is then achieved with traditional ray marching into the texture volumes (whose external bounds are defined by cube functions). This allows for cool tricks such as smooth implicit blending to get nice looking deformations, e.g. taking the smooth minimum between nearby/connected volumes. I started to investigate automatically splitting up models into smaller distance transform volumes for each animated bone, but sadly I wasn't able to publish these results into my thesis due to time constraints. For future researchers who stumble on this page with the goal of animating lots of volumetric content, I recommend looking into implicit surfaces above traditional sparse voxel octrees.

Citation

Please cite the thesis with:

@phdthesis{willcocks-2013-sparse-volumetric-deformation,
  title  = {Sparse Volumetric Deformation},
  author = {Chris G. Willcocks},
  year   = {2013},
  school = {Durham University},
  url    = {http://etheses.dur.ac.uk/8471/},
}

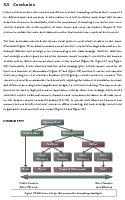
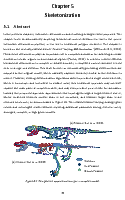
Feature-varying skeletonization

Intuitive control over the target feature size and output skeleton topology

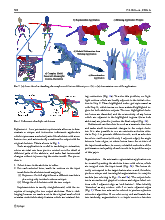
Click to go to full publication on Springer Link.

Abstract

Current skeletonization algorithms strive to produce a single centered result which is homotopic and insensitive to surface noise. However, this traditional approach may not well capture the main parts of complex models, and may even produce poor results for applications such as animation. Instead, we approximate model topology through a target feature size ω, where undesired features smaller than ω are smoothed, and features larger than ω are retained into groups called bones. This relaxed feature-varying strategy allows applications to generate robust and meaningful results without requiring additional parameter tuning, even for damaged, noisy, complex, or high genus models.

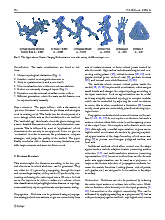
Overview

Given an input dense 3D mesh, it presents an intuitive algorithm to iterateively contract the mesh into a skeleton.

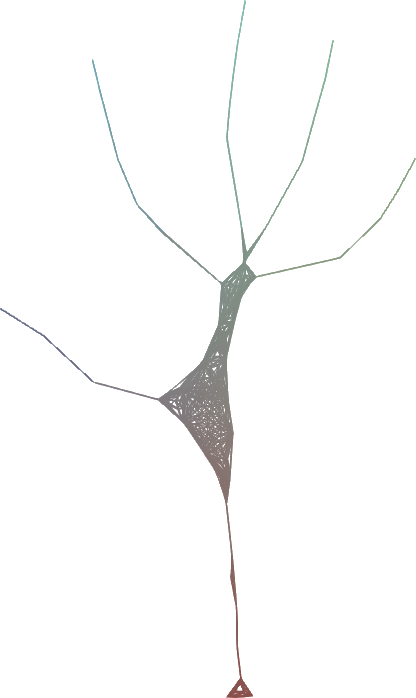
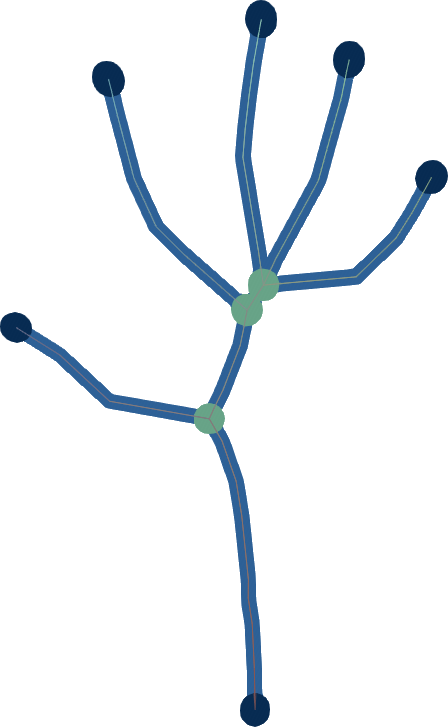
Simply, you have two forces:

You iteratively smooth the mesh, by moving the vertices to their average location in their original one-ring neighbourhood.
You iterateively merge the mesh, by moving the vertices to the average position of any nearby vertices within some fixed Euclidean distance ω.
- For very simple implementations, you can store vertex id's in a grid and fetch nearby grid cells; it works more-or-less the same.

The final force that contracts the mesh is a simple linear interpolation between 1. and 2. governed by the one-ring neighbourhood surface area.

While there are now better ways to generate curve skeletons, the nice little contribution with this at the time was its simplicity, and that it can make skeletons that are useful for animation with just a single parameter to adjust.

Key Advantages:

• Simplicity
• Speed
• Low parameters

It would be nice if this approach could be extended to the imaging domain; I briefly tried expressing similar concepts to the merging and smoothing with convolutions and got some interesting results, but I was unable to stop the skeleton overcontracting. The reason it stops overcontracting in the mesh geometry is because of perhaps an unexpected artifact whereby the vertices get pulled into groups > ω. This is also a limitation of the method, in that the vertices can contract in an unpredictable way impacting the skeleton quality. I haven't thought much about extending this.

Citation

Please cite the paper:

@article{willcocks-2012-feature-varying-skeletonization,
   author    = {Chris G. Willcocks and Frederick W. B. Li},
   title     = {Feature-varying skeletonization - Intuitive control over the target feature size and output skeleton topology},
   journal   = {The Visual Computer},
   volume    = {28},
   number    = {6-8},
   pages     = {775--785},
   year      = {2012},
   url       = {http://dx.doi.org/10.1007/s00371-012-0688-x},
   doi       = {10.1007/s00371-012-0688-x}
}

[return to top]